Calculus
This award-winning course is a robust, engaging, interactive, and student-friendly immersion into calculus. In this course, students begin a journey of calculus discovery and development that suits all learning styles with auditory, visual, and hands-on components throughout. Calculus 12 provides students a foundation for progression into University Calculus.
Within this course, students are led through the historical journey of the discovery and development of calculus. Each lesson involves interactive videos that allow students to go at their own speed, with the ability to pause and rewind at any point. With student-friendly note packages and practice questions with detailed solutions, students will never get stuck and can learn how to solve even the most challenging calculus problems. Students can also retake every quiz and test to encourage them to strive towards mastery.
Note: To learn more about AP Calculus options check out our AP Calculus AB and AP Calculus BC – where your students can earn college credit.
Table of Contents
*Each lesson is designed to take 60 – 90 minutes to complete with the exception of major projects and assignments.
Lesson 1: Introduction to Calculus
Lesson 2: Review of Function Terminology And More
Lesson 3: Graphing Calculators
Lesson 4: Compositions and Transformations of Functions
Lesson 5: Some Common Functions
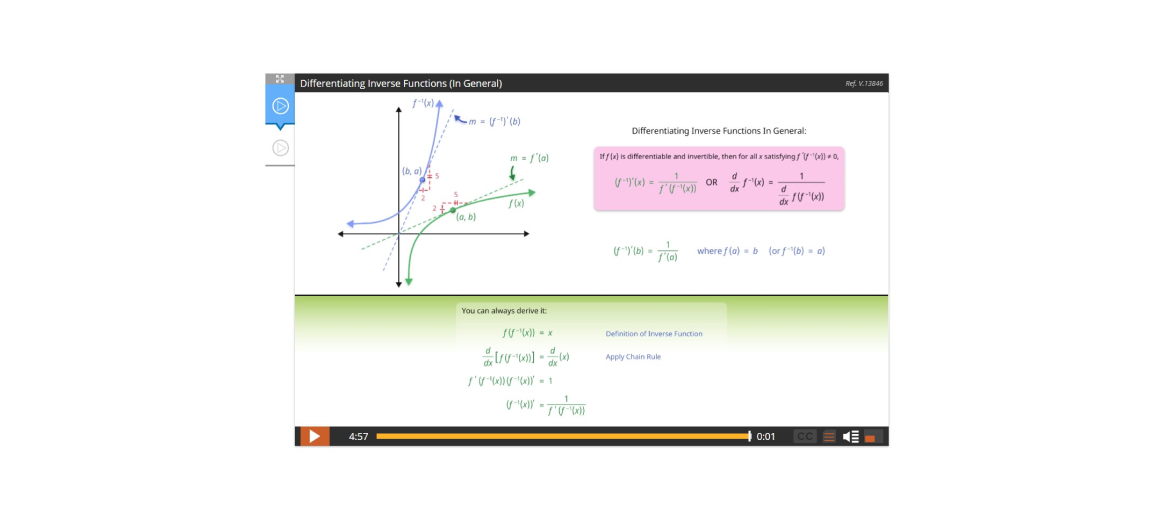
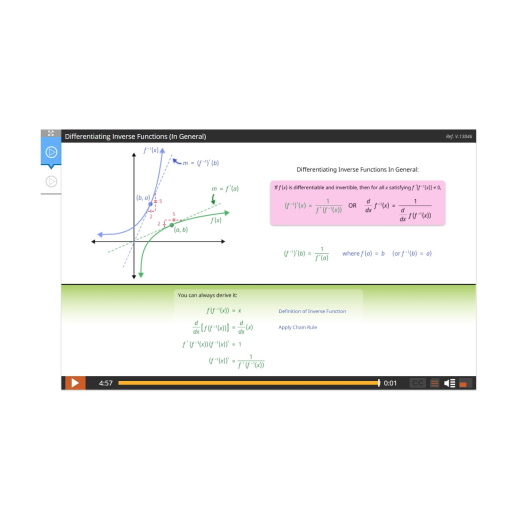
Lesson 6: Inverse Functions
Lesson 7: Exponential and Logarithmic Functions
Lesson 2: Review of Function Terminology And More
Lesson 3: Graphing Calculators
Lesson 4: Compositions and Transformations of Functions
Lesson 5: Some Common Functions
Lesson 6: Inverse Functions
Lesson 7: Exponential and Logarithmic Functions
Lesson 1: Introduction to Limits
Lesson 2: Properties of Limits
Lesson 3: Limits Involving Infinity
Lesson 4: Continuity and The Sandwich Theorem
Lesson 5: Applications of Limits
Lesson 2: Properties of Limits
Lesson 3: Limits Involving Infinity
Lesson 4: Continuity and The Sandwich Theorem
Lesson 5: Applications of Limits
Lesson 1: The Derivative
Lesson 2: Rules of Differentiation
Lesson 3: Trigonometric Derivatives and The Chain Rule
Lesson 4: Derivatives of Exponential, Logarithmic, and Inverse Trig Functions
Lesson 5: Implicit Differentiation
Lesson 2: Rules of Differentiation
Lesson 3: Trigonometric Derivatives and The Chain Rule
Lesson 4: Derivatives of Exponential, Logarithmic, and Inverse Trig Functions
Lesson 5: Implicit Differentiation
Lesson 1: Analyzing Functions Part I: Curve Sketching
Lesson 2: Analyzing Functions Part II: Maximums and Minimums
Lesson 3: Applied Maximum and Minimum Problems
Lesson 4: Distance, Velocity, Acceleration, and Rectilinear Motion
Lesson 5: Related Rates
Lesson 6: The Mean-Value Theorem and L’Hopital’s Rule
Lesson 2: Analyzing Functions Part II: Maximums and Minimums
Lesson 3: Applied Maximum and Minimum Problems
Lesson 4: Distance, Velocity, Acceleration, and Rectilinear Motion
Lesson 5: Related Rates
Lesson 6: The Mean-Value Theorem and L’Hopital’s Rule
Lesson 1: Area Approximation and Riemann Sums
Lesson 2: Introduction to the Definite Integral
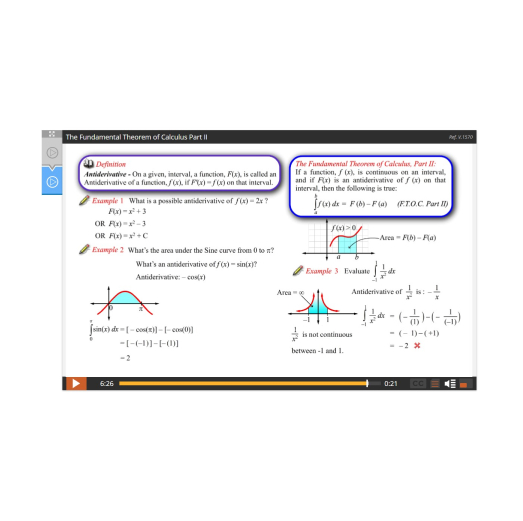
Lesson 3: The Fundamental Theorem of Calculus
Lesson 4: Integrals and Antiderivatives
Lesson 5: Integration by Substitution
Lesson 6: Integration by Parts
Lesson 7: The Definite Integral
Lesson 2: Introduction to the Definite Integral
Lesson 3: The Fundamental Theorem of Calculus
Lesson 4: Integrals and Antiderivatives
Lesson 5: Integration by Substitution
Lesson 6: Integration by Parts
Lesson 7: The Definite Integral
Lesson 1: Finding The Area Under and Between Curves
Lesson 2: Volume by Discs (Slicing)
Lesson 3: Volume by Shells
Lesson 4: Work
Lesson 5: Average Value of a Function and Rectilinear Motion Revisited
Lesson 2: Volume by Discs (Slicing)
Lesson 3: Volume by Shells
Lesson 4: Work
Lesson 5: Average Value of a Function and Rectilinear Motion Revisited
Lesson 1: Differential Equations – An Introduction
Lesson 2: Initial Value Problems, Slope Fields, and Euler’s Method
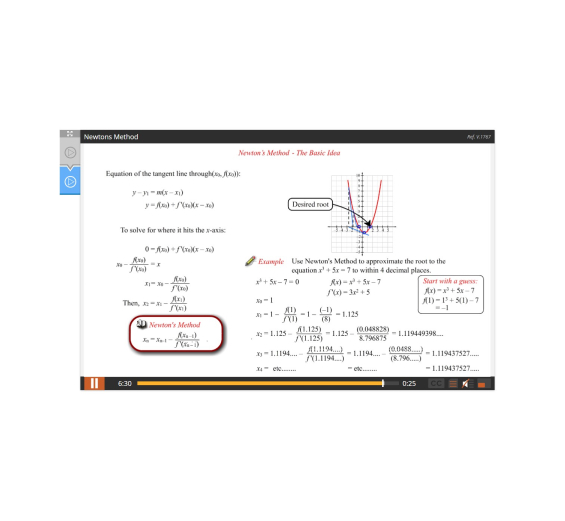
Lesson 3: Linearization and Newton’s Method
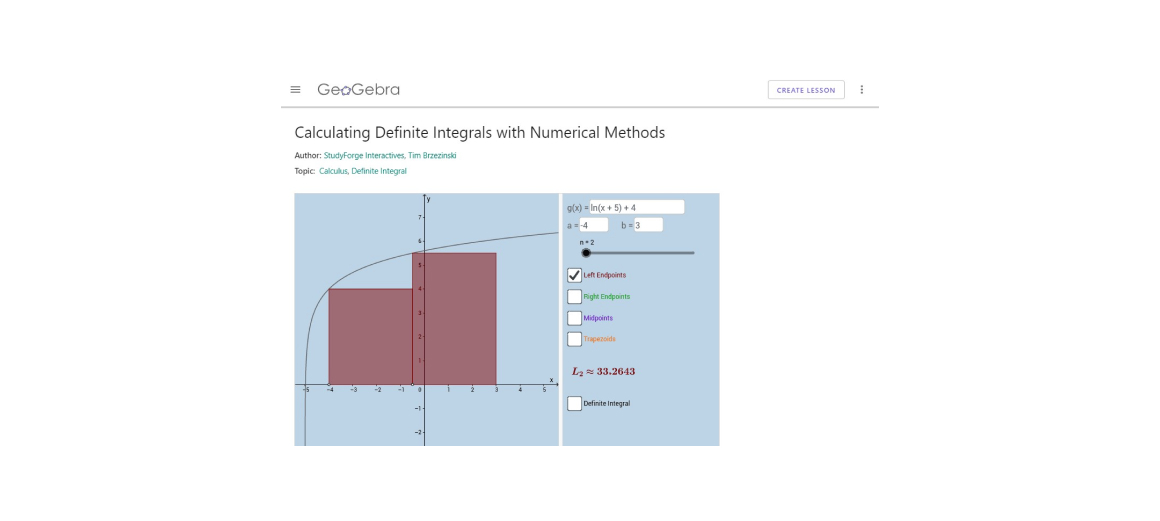
Lesson 4: Numerical Approximation Methods with Integrals
Lesson 2: Initial Value Problems, Slope Fields, and Euler’s Method
Lesson 3: Linearization and Newton’s Method
Lesson 4: Numerical Approximation Methods with Integrals
Experience a lesson as your students would
Don’t Take Our Word for It!
See What Others Have to Say:
I have been using the Study Forge math videos for a year now as part of my blended classroom. The benefits were immediate as I was able to free up the time spent with my students to better track their progress and construct personalized learning goals. My students love the ease of use of the system and most of all, the increase in their test scores! I can’t ever imagine going back to a traditional classroom!
SCOTT
Blended Ed Teacher
“The course was great! The videos used to teach much of the course material were engaging and easy to follow, and I found that they helped me to learn faster and more effectively than the usual textbook-based approach. Also, the applets included in many of the lessons provided a hands-on way for me to visualize and interact with the concepts being taught, which greatly increased my understanding of those concepts.”
VIHAAN
Calculus Student
I have to say this course was the best online course I have taken! The StudyForge program was beyond amazing.
Kim
Calculus Student
I just want to thank you for teaching me this year. It’s been great and I have learned a lot. Feedback of the final exam: very straightforward and very fair as you said… It is a good exam.
Jerry
Calculus Student
Course Features
- Many lessons include fun, interactive applets and dynamic graphs which help foster a conceptual and even intuitive understanding of fundamental topics.
- Digital DESMOS Graphing Calculator within the course