AP Calculus BC
This course aligns with the learning outcomes for:
AP Course (All regions)
This course aligns with the learning outcomes for:
AP Course (All regions)
Within this course, students are led through the historical journey of the discovery and development of calculus. Each lesson involves interactive videos that allow students to go at their own speed, with the ability to pause and rewind at any point. With student-friendly note packages and practice questions with detailed solutions, students will never get stuck and can learn how to solve even the most challenging calculus problems. Students can also retake every quiz and test, which are randomized, to encourage them to strive towards mastery.
Some question if online AP students can score high enough on their exams to receive college credit and placement. Students using StudyForge have done very well, even scoring on AP Calculus BC 12% above average, and our AP Calculus AB students scoring 41% higher than average on their AP test scores. However, if you narrow it down to the subset of students who had a certain minimum level of healthy interaction with the curriculum, the numbers skyrocket. Download our Whitepaper below to see how at one school, 100% of these engaged students passed the AP exam, with an 88% chance of becoming “very well qualified” (4) or “extremely well qualified” (5).
Some question if online AP students can score high enough on their exams to receive college credit and placement. Students using StudyForge have done very well, even scoring on AP Calculus BC 12% above average, and our AP Calculus AB students scoring 41% higher than average on their AP test scores. However, if you narrow it down to the subset of students who had a certain minimum level of healthy interaction with the curriculum, the numbers skyrocket. Download our Whitepaper below to see how at one school, 100% of these engaged students passed the AP exam, with an 88% chance of becoming “very well qualified” (4) or “extremely well qualified” (5).

Learn how using StudyForge sustained AP exam scores 41% better than the average classroom over 5 years.
GET THE FREE WHITEPAPER
AP Calculus BC covers the first two semesters of University Calculus (Calc 1 and Calc 2). It includes the topics covered in our AP Calculus AB course with the addition of parametric functions, polar functions, vector functions and analysis of series. Students will have the option to complete the AP Exam administered by the College Board and receive university credit.
Note: AP Calculus BC only differs from AP Calculus AB in scope, not difficulty. For more information on the topics covered in AP Calculus AB, click here.
Note: AP Calculus BC only differs from AP Calculus AB in scope, not difficulty. For more information on the topics covered in AP Calculus AB, click here.
What is AP?
Want to give your students a taste of college in the comfort of high school? By taking AP courses your students can develop their college skills, such as time management and critical thinking, all the while discovering their passions by studying subjects more in-depth.
Why Should Your Students Take AP Courses?
Want to give your students a taste of college in the comfort of high school? By taking AP courses your students can develop their college skills, such as time management and critical thinking, all the while discovering their passions by studying subjects more in-depth.
Why Should Your Students Take AP Courses?
- Earn College Credit
- Save Money by Skipping Introductory Courses in College
- Graduate Early
- Stand out in College applications
- Get approved to teach AP courses via College Board – Register your school with the College Board and complete the online AP Participation form. Click here to find out what this entails.
- You’ve been approved – Congratulations, now what? See this pdf on how to set up, enroll and order for your AP classroom.
- Start teaching! You will receive all materials, practice tests, and note packages your students need when they are enrolled in StudyForge class.
- Don’t Forget to Order your Exams by Nov 15th for all full-year and first-semester courses or Mar 15th for all courses that begin after Nov 15th.
- See all Teacher/Administrator resources at AP Central.
Table of Contents
*Each lesson is designed to take 60 – 90 minutes to complete with the exception of major projects and assignments.
Lesson 1: Introduction to Calculus
Lesson 2: Review of Function Terminology And More
Lesson 3: Graphing Calculators
Lesson 4: Compositions and Transformations of Functions
Lesson 5: Some Common Functions
Lesson 6: Inverse Functions
Lesson 7: Exponential and Logarithmic Functions
Lesson 2: Review of Function Terminology And More
Lesson 3: Graphing Calculators
Lesson 4: Compositions and Transformations of Functions
Lesson 5: Some Common Functions
Lesson 6: Inverse Functions
Lesson 7: Exponential and Logarithmic Functions
Lesson 1: Introduction to Limits
Lesson 2: Properties of Limits
Lesson 3: Limits Involving Infinity
Lesson 4: Continuity and The Sandwich Theorem
Lesson 5: Applications of Limits
Lesson 2: Properties of Limits
Lesson 3: Limits Involving Infinity
Lesson 4: Continuity and The Sandwich Theorem
Lesson 5: Applications of Limits
Lesson 1: The Derivative
Lesson 2: Rules of Differentiation
Lesson 3: Trigonometric Derivatives and The Chain Rule
Lesson 4: Derivatives of Exponential, Logarithmic, and Inverse Trig Functions
Lesson 5: Implicit Differentiation
Lesson 2: Rules of Differentiation
Lesson 3: Trigonometric Derivatives and The Chain Rule
Lesson 4: Derivatives of Exponential, Logarithmic, and Inverse Trig Functions
Lesson 5: Implicit Differentiation
Lesson 1: Analyzing Functions Part I: Curve Sketching
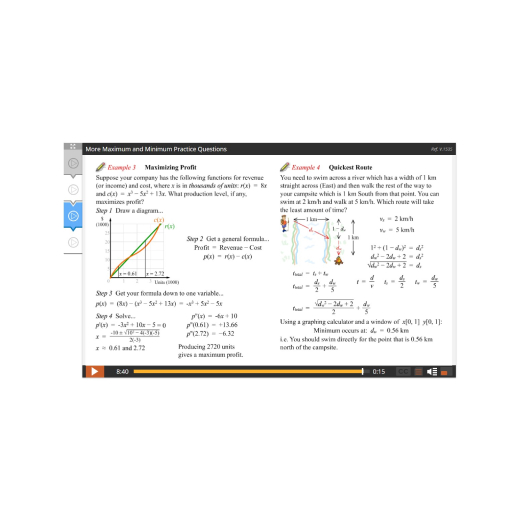
Lesson 2: Analyzing Functions Part II: Maximums and Minimums
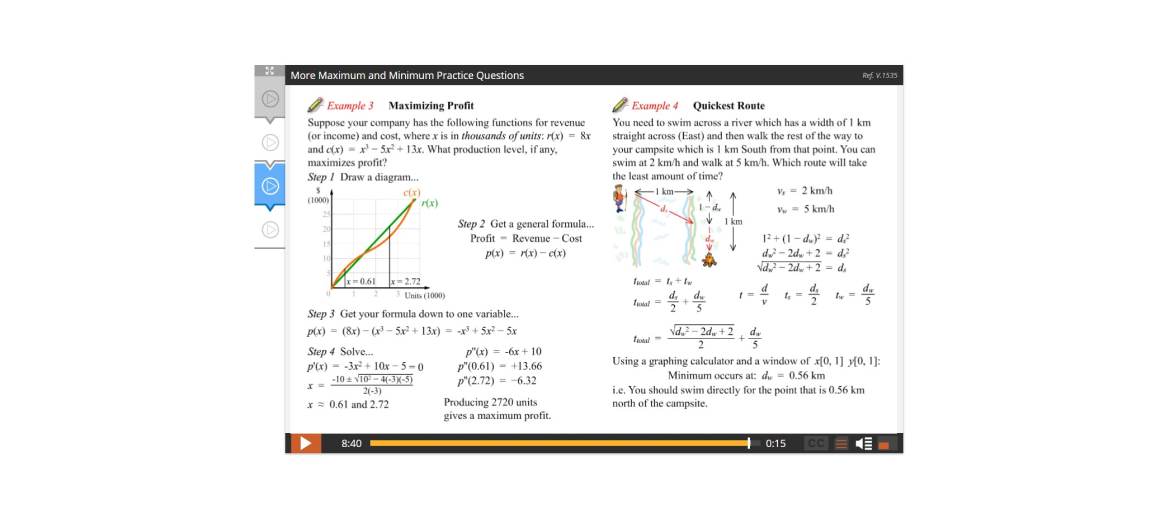
Lesson 3: Applied Maximum and Minimum Problems
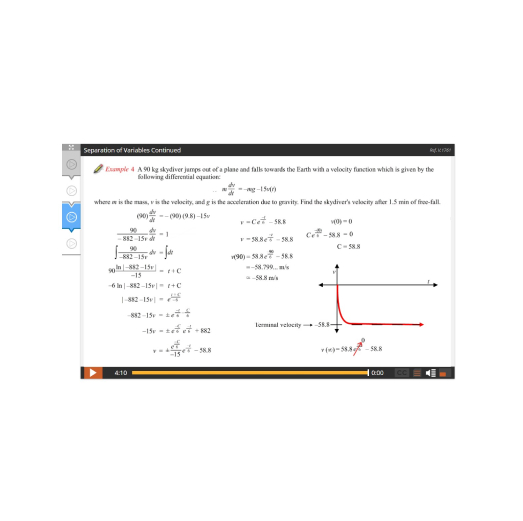
Lesson 4: Distance, Velocity, Acceleration, and Rectilinear Motion
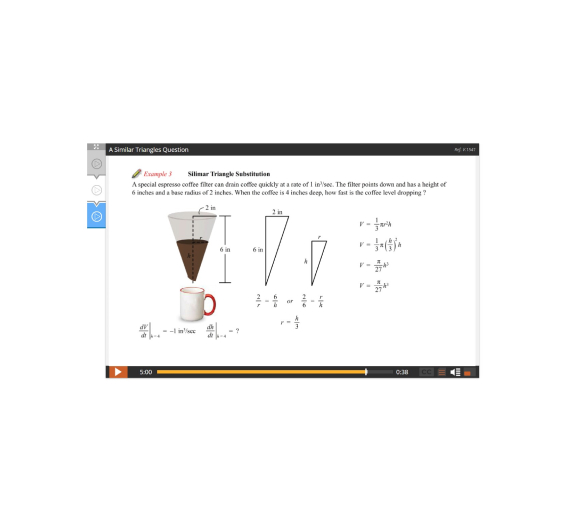
Lesson 5: Related Rates
Lesson 6: The Mean-Value Theorem and L’Hopital’s Rule
Lesson 7: Practice Test
Lesson 2: Analyzing Functions Part II: Maximums and Minimums
Lesson 3: Applied Maximum and Minimum Problems
Lesson 4: Distance, Velocity, Acceleration, and Rectilinear Motion
Lesson 5: Related Rates
Lesson 6: The Mean-Value Theorem and L’Hopital’s Rule
Lesson 7: Practice Test
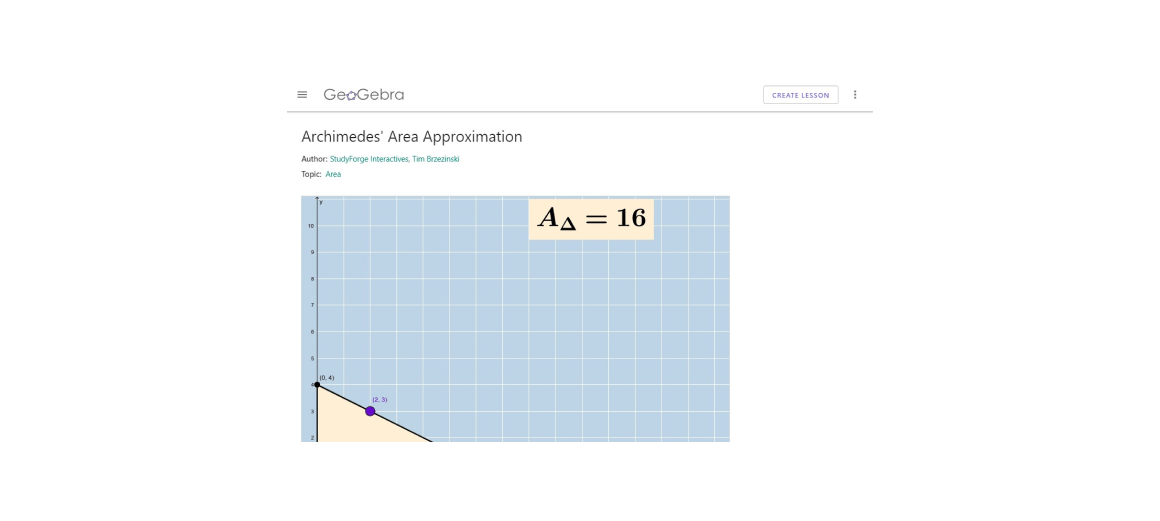
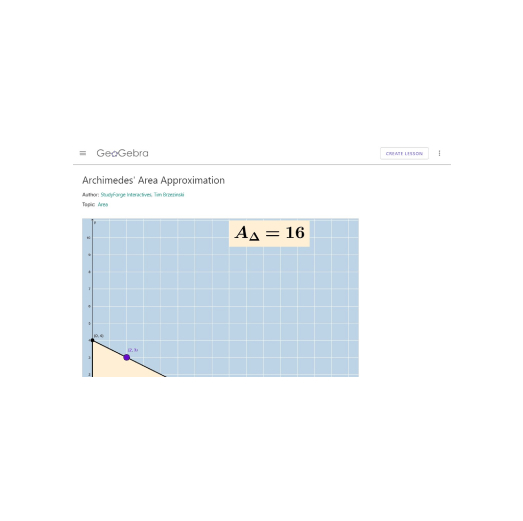
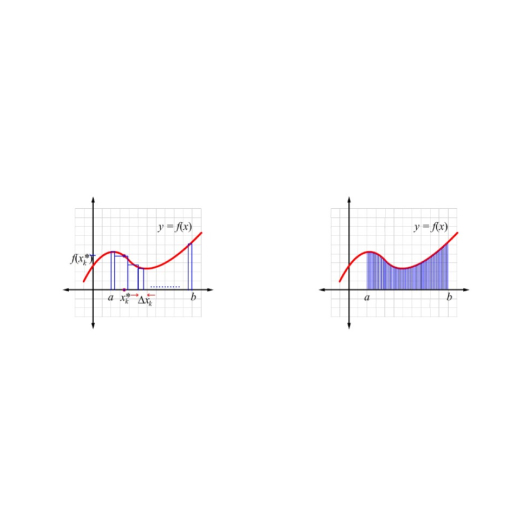
Lesson 1: Area Approximation and Riemann Sums
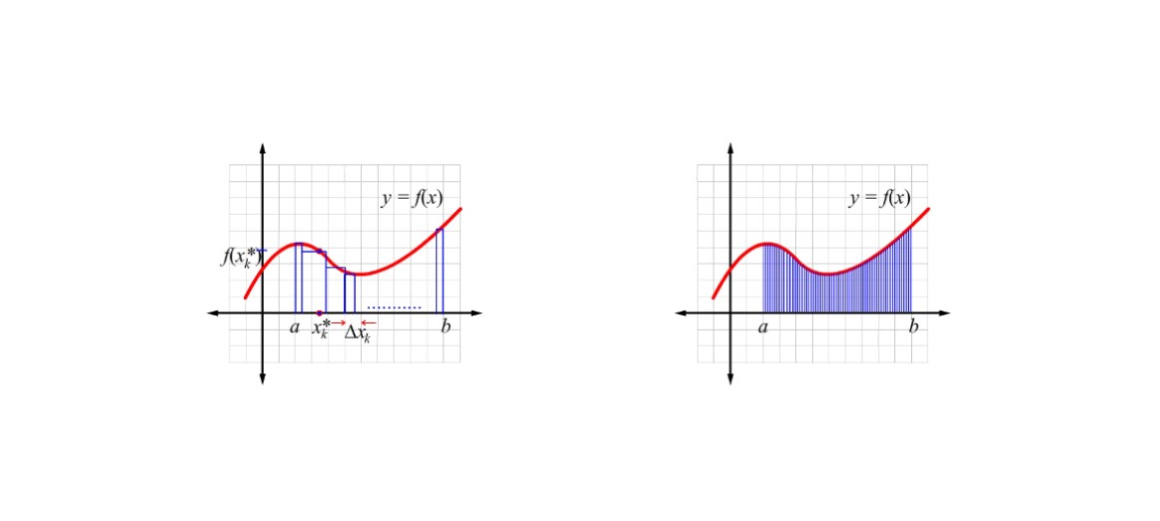
Lesson 2: Introduction to the Definite Integral
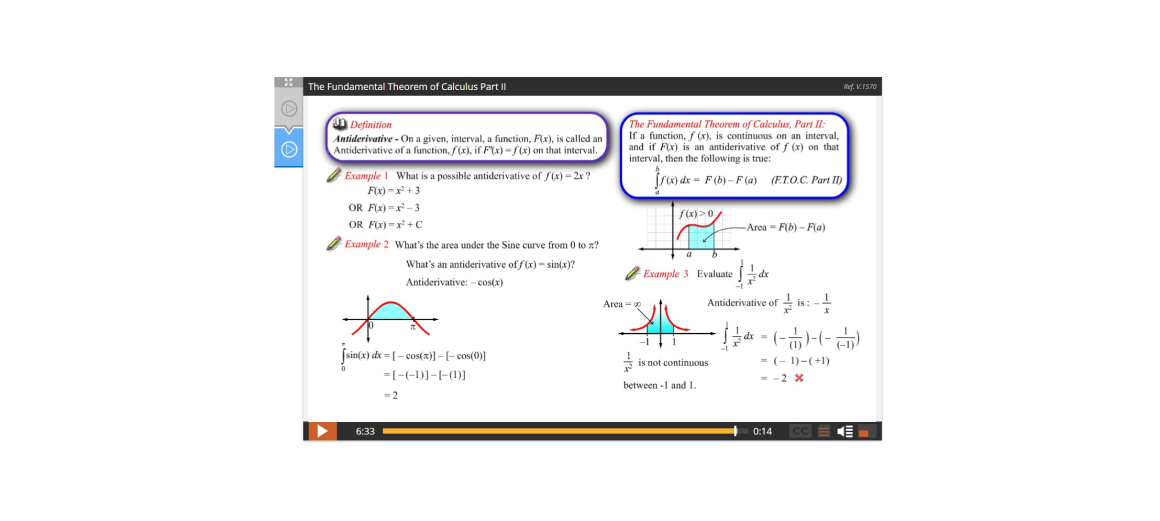
Lesson 3: The Fundamental Theorem of Calculus
Lesson 4: Integrals and Antiderivatives
Lesson 5: Integration by Substitution
Lesson 6: Integration by Parts – Optional
Lesson 7: The Definite Integral
Lesson 2: Introduction to the Definite Integral
Lesson 3: The Fundamental Theorem of Calculus
Lesson 4: Integrals and Antiderivatives
Lesson 5: Integration by Substitution
Lesson 6: Integration by Parts – Optional
Lesson 7: The Definite Integral
Lesson 1: Finding The Area Under and Between Curves
Lesson 2: Volume by Discs (Slicing)
Lesson 3: Volume by Shells
Lesson 4: Work
Lesson 5: Average Value of a Function and Rectilinear Motion Revisited
Lesson 2: Volume by Discs (Slicing)
Lesson 3: Volume by Shells
Lesson 4: Work
Lesson 5: Average Value of a Function and Rectilinear Motion Revisited
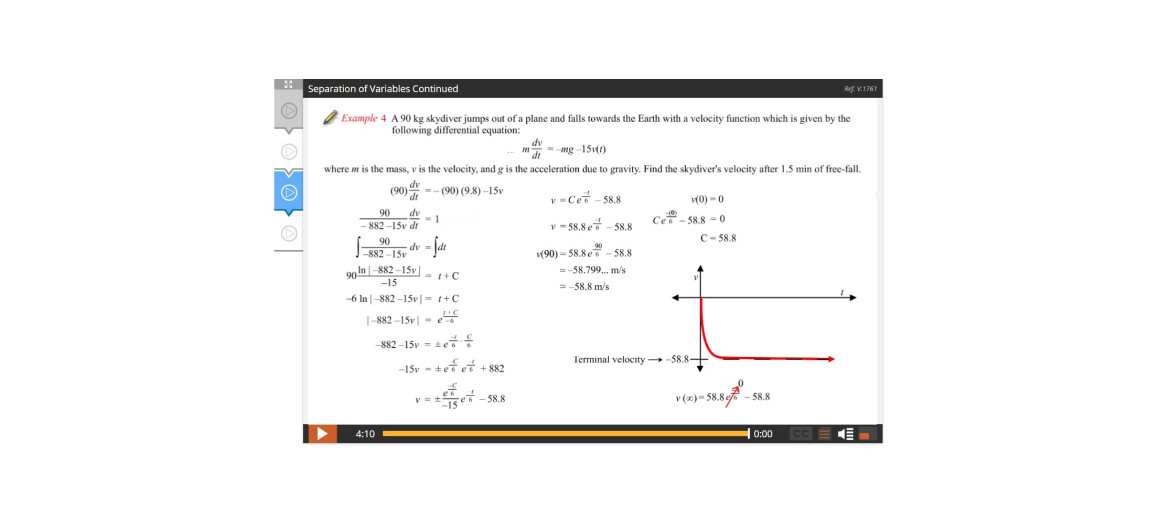
Lesson 1: Differential Equations – An Introduction
Lesson 2: Initial Value Problems, Slope Fields, and Euler’s Method
Lesson 3: Linearization and Newton’s Method
Lesson 4: Numerical Approximation Methods with Integrals
Lesson 2: Initial Value Problems, Slope Fields, and Euler’s Method
Lesson 3: Linearization and Newton’s Method
Lesson 4: Numerical Approximation Methods with Integrals
Lesson 1: Exploring the Graphs of f, f’, and f” (Revisited)
Lesson 2: Relative Rates of Growth
Lesson 3: Using Calculus With Data in a Table
Lesson 4: Functions Defined By Integrals
Lesson 5: Integration by Parts (Review) – Optional
Lesson 6: Integrating Using Partial Fractions – Optional
Lesson 7: Improper Integrals – Optional
Lesson 2: Relative Rates of Growth
Lesson 3: Using Calculus With Data in a Table
Lesson 4: Functions Defined By Integrals
Lesson 5: Integration by Parts (Review) – Optional
Lesson 6: Integrating Using Partial Fractions – Optional
Lesson 7: Improper Integrals – Optional
Lesson 1: Parametric Curves
Lesson 2: Polar Curves
Lesson 3: Vector Curves
Lesson 4: Length of Planar Curves
Lesson 5: Area of Planar Curves (Polar Curves only)
Lesson 2: Polar Curves
Lesson 3: Vector Curves
Lesson 4: Length of Planar Curves
Lesson 5: Area of Planar Curves (Polar Curves only)
Lesson 1: Series
Lesson 2: Convergence
Lesson 3: Tests for Convergence Part I
Lesson 4: Tests for Convergence Part II
Lesson 5: Error Bound
Lesson 2: Convergence
Lesson 3: Tests for Convergence Part I
Lesson 4: Tests for Convergence Part II
Lesson 5: Error Bound
Lesson 1: Maclaurin Series
Lesson 2: Taylor Series and Error Bound
Lesson 3: Power Series
Lesson 4: Radius and Interval of Convergence
Lesson 5: Applications of Polynomial Series
Lesson 2: Taylor Series and Error Bound
Lesson 3: Power Series
Lesson 4: Radius and Interval of Convergence
Lesson 5: Applications of Polynomial Series
Lesson 1: Roller Coaster Project Part I
Lesson 2: Roller Coaster Project Part II
Lesson 3: Fish Stock Populations Project
Lesson 2: Roller Coaster Project Part II
Lesson 3: Fish Stock Populations Project
Experience a lesson as your students would
Don’t Take Our Word for It!
See What Others Have to Say:
After my students had been using the StudyForge AP Calculus Curriculum I was thrilled as the number of students who scored a “5/5” on the AP exam almost doubled! – But I am even more thrilled now after discovering the reporting tools they have created to empower me as an online teacher!
JOYCE
Online AP Calculus Teacher at Sevenstar Academy
I think the videos are excellent. Unlike lectures, I can actually rewind back and forth as much as I want. In class, students kind of miss important information because they are busy writing notes.
Alice
AP Calc Student
This course prepared me well because I was able to get a 5/5 on the College Board Exam…
Nick
AP Calc Student
I love the course! I like how it’s really simple to understand and how everything is organized and it’s easy to access resources.
Alina
AP Calc Student
Course Features
- Many lessons include fun, interactive applets and dynamic graphs which help foster a conceptual and even intuitive understanding of fundamental topics.
- Digital DESMOS Graphing Calculator within the course